Accueil Forum Mail Livre d'OR

Chapitres

COMPORTEMENTS ASYMTPOTIQUES

I- Limites en +∞ ou en -∞

Dans ce paragraphe, nous allons nous servir deux deux réels, qui seront désignés par les lettres "a" et "l" et un nombre entier "n", supérieur ou égal à 1.

définition
Soit f une fonction, définie sur un intervalle [a; +∞[. Dire que f(x) tend vers +∞, signifie que les valeurs de f(x) sont de plus en plus grandes, tant que x augmente. On écrit: limx->+∞f(x) = +∞ ou lim+∞f = +∞.

exemples

f a pour limite -∞ en +∞ limx->+∞f(x) = -∞	f a pour limite +∞ en -∞ limx->-∞f(x) = +∞	f a pour limite -∞ en -∞ limx->-∞f(x) = -∞

Les plus intelligents d'entre vous ont donc déja noter que les fonctions trigonométriques n'avaient pas de limite car le cossinus ou le sinus de x est toujours compris entre -1 et 1, elles sont bornées sur R.

Limite finie
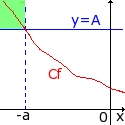
Dire que f tend vers le réel l lorsque x tend vers +∞ signifie que les valeurs de f(x) se rapprochent de l tant que x augmente On écrit limx->+∞f(x)=l ou lim +∞ f = l.

Sur ce schéma,on voit que plus le nombre x est grand, plus f(x) se rapproche de l.

Asymptote horizontale:

Lorsque lim_x->+∞ f(x) = l, on dit que la droite d'équation y = l est asymptote à la courbe C_f d'équation y = f(x) en +∞ (ou en -∞)

C'est la droite dont la courbe C_f se rapproche de plus en plus sans pour autant la toucher, et ce quel que soit x.

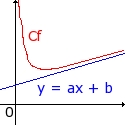
Asymptote oblique:

On dit que la droite D d'équation y = ax+b est asymptote à la courbe C_f en +∞ (ou en -∞) lorsque:
lim_x->+∞[f(x) - (ax + b)] = 0 ou lim_x->-∞[f(x) - (ax + b)] = 0

exemples d'asymptotes

Voilà, j' prends tellement soin de mes "élèves" que je vous ai concocté deux petits schémas, mais c'est du "fait maison", alors pas de commentaires ok? je ne sais pas si je vous l'ai déjà dis mais moi je préfère coder et programmer que de faire des schémas et je vous avoue franchement que le mot graphique me donne des boutons, mais bon là c'est différent, c'est pour mes "élèves", on dit merci Arn@Üde...xD

assymptote horizontale	asymptote oblique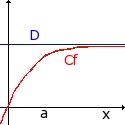

II- Limite infinie en un réel a

Comme vous l'avez tous deviner (en tout cas ce qui ont lu le titre) dans ce paragraphe, a va désigner un réel et b un réel strictement positif

Définition

Soit f une fonction définie sur un ensemble Df contenant l'intervalle ]a; a+b[ ou l'intervalle ]a-b; a[. Dire que f(x) tend vers a signifie que les valeurs de f(x) augmente sans arrèts tant qu'on se rapproche de a, en restant dans Df. On écrit limx->af(x) = +∞. Il en va de même pour une limite en a égale à -∞

Dans la majorité des cas, c'est des fontions de la forme 1/x qui admettent une limite égale à +∞ ou -∞ en un réel.

Dans certains exercices, il vous sera utile de faire ce qui suit, à savoir opérer un changement de variables, atta atta, c'est koi ton truc là?
Ah oups ba je ne sais pas si vous comprenez le français mais quand on dit un changement de variables, c'est que quelque part, on a changer une variable! logique non?

Alors voilà coment on s'y prend:
On pose x = a+h, ce qui veut dire concrètement que dans votre expression, f(x) sera remplacé par f(a+h), ainsi
lim_x->af(x) = lim_h->0f(a+h).

asymptote verticale

Définition
Si la limite en a de f est infinie, on dit que la droite d'équation x=a est asymptote verticlale de la courbe représentente de f. Ce qui me permet de clarifier un point tout de suite (il n'est jamais trop tard pour bien faire...) une droite est asymptote à la courbe représentative d'une fonction mais surtout pas à la fonction elle-même!!!

III- opérations sur les limites

Ah!!!! enfin une partie ou il n'y a que du cours et de la bonne vieille formule hum!!!!!!

a va désigner soit un réel, soit +∞ soit -∞. l et l' désignent des réels...Et je vais vous demander d'admettre les théorème suivants:

limite de f + g

si limx->af(x)=	l	l ou +∞	l ou -∞	+∞
et limx->ag(x)=	l'	+∞	-∞	-∞
alors limx->a(f + g)(x)=	l + l'	+∞	-∞	on ne peut pas conclure directement

limite de f x g

si limx->af(x)=	l	l > 0 ou +∞	l < 0 ou -∞	l > 0 ou +∞	l < 0 ou -∞	0
et limx->ag(x)=	l'	+∞	+∞	-∞	-∞	+∞ ou -∞
alors limx->a(f x g)(x)=	l x l'	+∞	-∞	-∞	+∞	on ne peut pas conclure directement

Dans le cas où l'une des limites est infinie, et l'autre non nulle, le produit est infini, le signe dépens de la règle du signe d'un produit dans R.

limite de 1/g

si limx->ag(x)=	l différent de 0	l=0 et g>0	l=0 et g<0	+∞ ou -∞
alors, limx->a1/g(x)=	l'	+∞	-∞	0

Pour obtenir la limite d'un quotion du type (f/g)(x), on décompose ce quotient en f(x) x 1/g(x).

OUF!!!! pas facher que ce chapitre soit terminer non, pas vous?